Математика. 13 апреля

Тема: Задачи на движение в одном направлении “вдогонку”

Эту тему подсказал один путешественник, с которым недавно произошла вот такая история, когда он собирался в путешествие.

– Господин шкипер, здравствуйте!

Не поможете ли Вы мне? Дело в том, что я хотел отправиться в путешествие. Первую часть пути мы должны проплыть на паруснике, а потом пересесть на поезд и уехать в город Владивосток. Но я опоздал, и парусник отплыл без меня. Я созвонился с капитаном парусника. Он сказал, что ждать меня они уже не могли, и отплыли без меня. Сейчас они остановились в небольшом посёлке в 48 км отсюда. Но скоро отправляются дальше. Помогите, пожалуйста, догнать парусник как можно скорее. Ведь если я через 5 часов не догоню их, то опоздаю и на поезд. И тогда – конец моему путешествию.

– Ну что же, мы постараюсь Вам помочь, но для этого необходимо уточнить некоторые детали.

Вы сказали, что парусник находится в 48 км отсюда? А теперь узнайте у капитана парусника, с какой скоростью он движется?

– Да, я узнал – его скорость равна 6 км/ч.

– Так, хорошо. Скорость моего катера – 18 км/ч. Надо узнать, сколько времени понадобится катеру, чтобы догнать парусник. Для того, чтобы разобраться в ситуации, надо просто подумать… Давайте выполним рисунок.

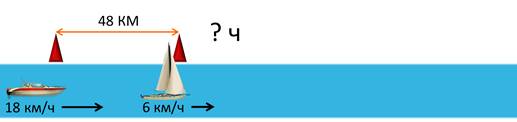
Итак, вот река. Вот здесь находимся мы, а вот, на расстоянии 48 км отсюда находится парусник. Скорость парусника 6 км/ч, скорость моего катера – 18 км/ч. Надо узнать, через сколько часов мы сможем догнать катер.

– Пожалуйста, давайте скорее поплывём, ведь парусник уже отплывает. А по пути и решим эту задачу.

– Ну что же, в путь.

– Итак, мы отплыли одновременно с парусником. Мы сейчас посчитаем, сколько времени нам понадобиться, чтобы доплыть до посёлка. Расстояние до посёлка 48 км разделим на скорость нашего катера – 18 км/ч.

48 : 18 =

– Да, но ведь парусник за это время далеко отплывёт от посёлка. Такой способ решения нам не подходит. Попробую нарисовать рисунок.

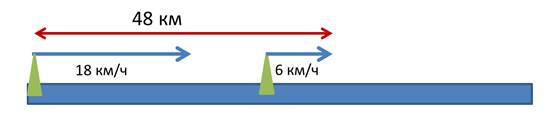
Так, вот река, вот место, откуда мы отплыли, а вот посёлок, откуда уже одновременно с нами отплыл парусник. Вот направление и скорость парусника и нашего катера.

Через час парусник проплывёт ещё 6 км, ведь его скорость 6 км/ч, а мы – 18 км (наша скорость 18 км/ч). Замечательно, расстояние между нами сократится. Пройдёт ещё час. Парусник отдаляется ещё на 6 км, но мы все равно становимся к нему ещё ближе. Я понял!!! За каждый час мы будем приближаться к паруснику на одинаковое количество километров. Ага, это наша скорость сближения. Сейчас я её узнаю. Мы догоняем парусник со скоростью18 км/ч, но за это время он уплывает на 6 км/ч.

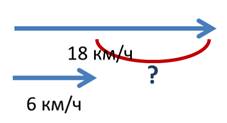
Значит, скорость сближения меньше нашей скорости на 6 км/ч. Мы от 18 – 6, получается 12 км/ч.

1) 18 – 6 = 12 (км/ч)

Это наша скорость сближения при движении вдогонку. Именно на столько за каждый час будет сокращаться расстояние между катером и парусником. Та-а-а-к. Я знаю, что расстояние между катером и парусником было 48 км, и теперь узнал, что скорость нашего сближения – 12 км/ч. Сейчас я найду время, за которое катер догонит парусник. Чтобы найти время, надо расстояние разделить на скорость.

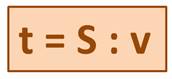
2) 48 : 12 = 4 (ч).

Ура! Я успею на поезд!

А вы знаете, мне так понравилось решать задачи на движение вдогонку. И теперь я не буду так переживать – ведь я знаю, что вовремя доплыву до пункта отправления поезда. Вы знаете, мне захотелось ещё решать такие задачи. Сейчас со своего телефона я зайду в интернет и попытаюсь найти ещё одну. Ага, вот и нашёл. Вот моя задача.

Пассажирский поезд отправился во Владивосток. Когда от станции отправления он отошёл на расстояние 342 км, от того же вокзала в том же направлении вышел скорый поезд. С какой скоростью шёл скорый поезд, если скорость пассажирского 50 км/ч, и скорый догнал его через 9 часов?

Да, нелёгкая задача. Но, как говорится, «просто надо подумать». И, конечно, изобразить всё на рисунке.

В задаче известно, что первоначально расстояние между поездами было 342 км, и скорый поезд догнал пассажирский за 9 ч, т. е. через 9 ч оно стало равно 0. У нас есть расстояние, и время, за которое это расстояние было сокращено до 0, т.е. поезда сблизились. Значит, мы можем найти скорость сближения поездов по формуле.

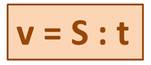
1) 342 : 9 = 38 (км/ч).

Это – скорость сближения поездов. А что такое «скорость сближения» при движении в одном направлении? Это разница между скоростями движущихся объектов. А, проще говоря, на сколько одна скорость больше другой. Скорый поезд, конечно, двигался быстрее пассажирского. И теперь мы знаем, на сколько быстрее – на 38 км/ч. Значит, мы можем узнать скорость скорого поезда. Мы к скорости пассажирского поезда прибавляем скорость сближения поездов.

2) 50 + 38 = 88 (км/ч).

Да неплохая скорость для поезда! Скоро я тоже поеду на таком. А пока могу решить ещё одну задачу. Вот, например, такую.

Из города А выехал мотоциклист, а из города Б одновременно с ним выехал велосипедист. Скорость мотоциклиста 80 км/ч, а скорость велосипедиста – 12 км/ч. Через 3 ч мотоциклист догнал велосипедиста. На каком расстоянии друг от друга находятся города А и Б?

Конечно, делаю рисунок.

Дорога, города А и Б, направление движения и скорость.

За один час мотоциклист проедет 80 км, а велосипедист – 12 км. При этом они сближаются. Вспомним, что при движении в одном направлении вдогонку скорость сближения равна разности скоростей.

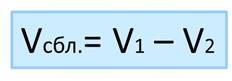
Находим её.

1) 80 – 12 = 68 (км/ч) – скорость сближения.

Нам известна скорость сближения и время, за которое мотоциклист догнал велосипедиста, т.е. преодолел то расстояние, которое было между ними первоначально. Вспоминаем формулу решения задач на движение.

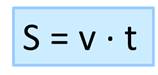
Чтобы найти расстояние, мы скорость умножаем на время. Выполняем действие:

2) 68 · 3 = 204(км). Вот мы и узнали расстояние между городами. Ответ: расстояние между городами 204 км.

Вот как здорово! Пока я решал задачи, мы догнали парусник и теперь я вместе со всеми отправлюсь в город Владивосток. Спасибо шкиперу за то, что он помог мне догнать моих друзей. А ещё я сегодня понял, что если два объекта движутся из разных точек в одном направлении вдогонку, то скорость сближения – это разность двух скоростей.

Надеюсь, ребята, что и вы разобрались с задачами на движение в одном направлении “вдогонку”. Для лучшего понимания, посмотрите ещё и видеоурок.

Теперь проверим, насколько вы поняли и усвоили данную тему. Для этого решите несколько задач в форме, размещённой чуть ниже. Обращаю внимание, что решение и ответ вы впечатываете прямо в данную форму. Когда решите все задачи, напишите свои фамилию и имя, не забудьте нажать кнопку “отправить”.

Хорошо. Второй урок посвятим повторению изученного.

1) Прорешать карточки на платформе Учи.ру  Математика – 4 класс – Площадь. + Математика – 4 класс – Задачи на движение – Движение навстречу и Движение в противоположных направлениях.

2) В тетради решить задания из учебника №883, №884, №895, №896, №913. Сфотографировать (фотографии должны быть чёткими, хорошо просматриваемыми), прислать на проверку по почте [email protected].